ZFS backups and other tidbits

It seems that OpenSolaris zfs has already got zfs backup and zfs restore commands. Our Solaris release doesn’t yet. Anyhow, backing up is simple, right?

We’ll perform the following steps:

• Snapshot the datasets once an hour. This can be done with the simplest of scripts, the hard part being a naming scheme for the backups.

  dataset = 'pool/something'
  name = Time.now.strftime("%Y%m%d%H%M")
  `zfs snapshot #{dataset}@#{name}`

• Sync the snapshots to another machine (hot standby) using zfs send and zfs receive with a good combination of the flags -I and -R. This is almost trivial as well. ZFS does a whole lot of work there for you, you just have to come up with what to sync where.

• And lastly, to prevent our pools from running full: Weed out snapshots we don’t want anymore, both in the backup and in the active set. This is what the remainder of the article is going to be about.

For all practical purposes, only the Grandfather-Father-Child scheme helps us in this situation. We don’t bother with the Towers of Hanoi even though that might be an algorithmic exercise worth it. It turns out that a generic GFC implementation is worth it as well.

The Grandfather-Father-Child (GFC) scheme sounds easy enough when presented. Let’s assume you want to keep 24 hourly , 7 daily, 12 monthly and 2 yearly backups around. This gives you a solid backlog for your data.

In the above setup, your backups will be named like this:

  pool/dataset@201004042200
  pool/dataset@201004042300
  pool/dataset@201004050000
  (... snippage ...)
  pool/dataset@201004050700
  pool/dataset@201004050800
  pool/dataset@201004050900

But to infuse a bit of real world in this problem description, here’s what’ll happen: Your administrator will snapshot any dataset at random before making an important change. He’ll either name this snapshot @pre_important_change or even @201004050907_important_change.

Another thing that will happen (as in Murphy says it does) is that your cronjob that does the snapshots will do so at irregular moments because of several factors (machine load, pesky users).

So here is a more realistic input to our algorithm:

  pool/dataset@201004042200
  pool/dataset@201004042301
  pool/dataset@201004050010
  (... snippage ...)
  pool/dataset@201004050705
  pool/dataset@201004050800
  pool/dataset@pre_important_change
  pool/dataset@201004050900
  pool/dataset@201004050907_important_change

So I was looking for something simple that could – in this context – apply rules like the ones above (24 hourly backups). After a bit of discussion with one of my coworkers we came up with something surprisingly simple given the irregularity of the problem.

I’ll express the algorithm as a method on something I will call a SnapshotSet, returning a new set containing the snapshots we want to keep. Here’s now you would use this:

  set = SnapshotSet.new([snapshot1, snapshot2, ...])
  
  keep = set.gpc(
    1.hour => 24, 
    1.day => 7)

This reduces the problem to this: Given a list of snapshots (each with a timestamp) and a list of (interval, count) tuples, find which snapshots should be kept.

The following is structured in two parts: What to do for each of the tuples and how to synthesize the resulting keep list.

For each (interval, count) tuple…

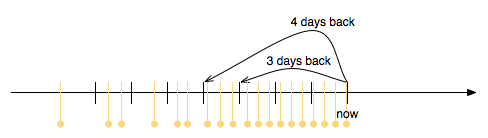
The image shows a timeline with snapshots in orange. Let’s say we want to find out which snapshots to keep to be able to provide 7 daily snapshots. ((1.day, 7)) To do this, we create a list of sample points starting 1 day ago, with step size of 1 day each. This is also drawn in the picture.

For each of those sample points the snapshot that is closest in time is kept. Look at this picture:

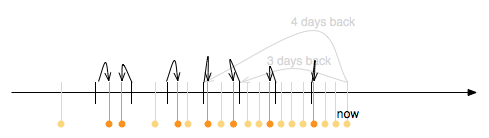
This procedure will yield at most 7 daily snapshots to keep in a best effort manner.

And how to synthesize the result

The resulting list of snapshots to keep can now be assembled by computing the union of all the snapshots that would have been kept for each tuple. This list completely covers what the rules specified.

Except that we probably don’t want to delete all the newest snapshots that the rules say nothing about, like the few ticks between 1 day ago and the now. So I’ll just say that all snapshots between now and the first tick of all tuples must be kept as well. (hand waving)

Conclusion

This three-step backup plan seems to work surprisingly well. If anyone is interested in some code, I think I could put this up on github – but I don’t want to add to the redundancy in the field ;). In this article I’ve shown how a simple Grandfather-Father-Child backup scheme could be made to work with real world input data.